Topologia: Bottiglia di Klein

La bottiglia di Klein è una superficie non orientabile (non ha un sopra ed un sotto. Vedi  http://pensierispettinatissimi.blogspot.it/2017/01/nastro-di-mobius-e-lorientabilita-il.html) ed è senza bordo.

“Fu introdotta dal matematico tedesco Felix Klein nel 1882 e la chiamò FLÄCHE, che significa superficie in tedesco. Siccome bottiglia di dice flasche, la parola venne tradotta erroneamente e, una volta adottato questo nome, fu impossibile correggerlo. Il fatto che la riproduzione tridimensionale ricordi la forma di una bottiglia contribuì nell'errore” (da “Forme che si deformano” di Vicente Muñoz) 

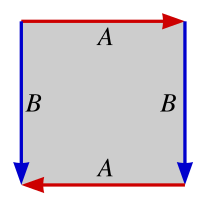
La bottiglia di Klein si ottiene da un quadrato identificando i lati come viene indicato nella seguente figura:

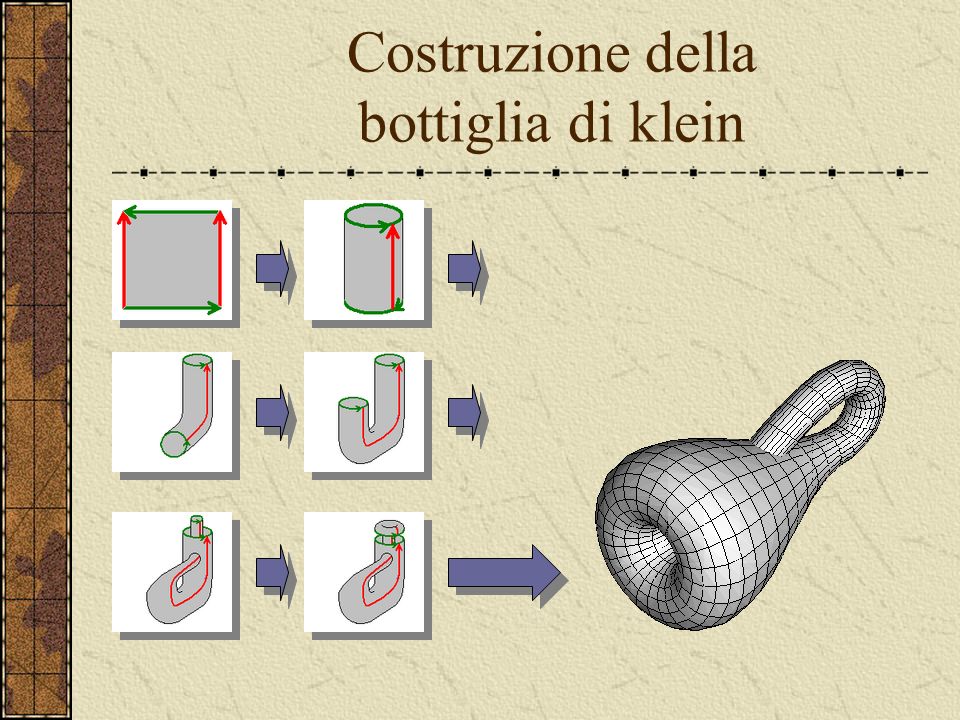
Se si identificano due lati opposti “per dritto” (cioè identificati i punti alla stessa altezza sui due lati verticali) e gli altri due nell'altro verso, si ottiene al primo passo un cilindro: poi, però, non si possono più semplicemente accostare le due circonferenze per incollarle, perché sulle due circonferenze è opposto il verso secondo cui vanno identificati i punti. Per riuscire a incollarle occorre allora “passare da dentro”, permettendo che la superficie si autointersechi.

Si tratta di una superficie ad una sola faccia, cioè con la proprietà che da qualunque punto sulla superficie si può raggiungere qualunque altro punto (esattamente come nel nastro di Möbius), ma con l'ulteriore interessante proprietà di essere una superficie chiusa, cioè priva di bordi. L'immersione della bottiglia nello spazio a tre dimensioni ha introdotto una linea di intersezione tra due parti della superficie. Quseto è dovuto alla circostanza che mentre il nastro di Möbius può essere rappresentato all'interno dello spazio euclideo tridimensionale , la bottiglia di Klein non può (e infatti nelle rappresentazioni grafiche tridimensionali la superficie è costretta ad autointersecarsi da qualche parte) ma può essere rappresentata nello spazio euclideo quadridimensionale .

Se tagliamo la bottiglia di Klein lungo una linea mediana otteniamo due nastri di Möbius: un altro modo di costruire la bottiglia è proprio quello di saldare due nastri di Möbius per il loro bordo. Il fatto che la bottiglia di Klein contenga nastri di Möbius è di particolare interesse: il nastro di Möbius può essere considerato come l'unità base delle superfici non orientabili (cioè con una sola faccia), in quanto si può provare che ogni superficie di questo tipo contiene un nastro di Möbius )