Nastro di Möbius e l'orientabilità

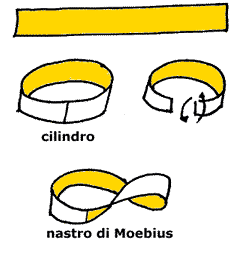
Il nastro di Möbius è costruito con una lunga striscia di carta, incollandone i bordi stretti dando mezzo giro a uno di essi.

Ha queste caratteristiche: 

- ha un solo bordo: se seguiamo un punto sul bordo e muoviamo il dito lungo lo stesso fino a tornare al punto segnato, percorreremo l’intero bordo 

- ha una sola faccia: se mettiamo un dito su una faccia e lo muoviamo lungo la stessa, arriviamo allo stesso punto toccando con il dito dall’altra parte. Pertanto tutti e due i lati del nastro di Möbius hanno la stessa faccia 

Il nastro è in altri termini una varietà non orientabile e non bicolorabile nello spazio tridimensionale. 

Per comprendere cosa s’intende per varietà non orientabile occorre considerare quanto segue “Anzitutto occorre chiarire il significato del termine varietà; in Geometria si studiano curve (oggetti di dimensione 1, hanno solo la lunghezza, ad esempio una circonferenza), superfici (oggetti di dimensione 2, ad esempio una superficie sferica), parti di volume (oggetti di dimensione 3, ad esempio la sfera intera). In generale, sebbene l'intuizione visiva venga meno, è possibile considerare superfici di dimensione n, che vengono dette varietà n-dimensionali. Dunque una varietà di dimensione 1 è una curva (non necessariamente piana), una varietà di dimensione 2 è un' intuitiva superficie, e così via. Ora pensiamo un attimo alla superficie laterale di un cilindro: la possiamo ottenere facilmente ritagliando da un foglio di carta una striscia rettangolare con un lato ben più corto dell'altro, e incollando i due lati uguali più corti del rettangolo. Ebbene, tale superficie è abbastanza ordinaria: infatti, come uno potrebbe ingenuamente pensare, tutte le superfici debbono avere 2 facce: un sopra ed un sotto” (tratto da “Oggetti matematici curiosi: le varietà non orientabili” di Luca Lusardi).

“Se immaginiamo di camminare sul lato esterno della superficie cilindrica, non riusciremo mai ad arrivare dall'altra parte senza attraversare il bordo”. Per rendersene conto “basta colorare la superficie cilindrica partendo da una delle 2 facce: se uno non attraversa il bordo, finisce con il colorare solo una delle 2 facce. Superfici di questo tipo si chiamano orientabili: ovvero hanno un sopra ed un sotto” (tratto da  “Oggetti matematici curiosi: le varietà non orientabili” di Luca Lusardi).

Il nastro  di contro è una superficie non orientabile. “Infatti, se proviamo a colorare il nastro partendo da un suo punto, quello che capita è che uno finisce con il colorare tutto il nastro senza attraversare il bordo. .. Dunque il nastro di Möbius ha una sola faccia. Se uno immagina di camminare su un Nastro di Möbius, dopo un certo tempo si ritrova esattamente al di sotto di dove era partito, senza aver dovuto per questo attraversare il bordo, o fare un buco lungo il percorso” (tratto da  “Oggetti matematici curiosi: le varietà non orientabili” di Luca Lusardi).

Immagine di Escher

Tagliando il nastro a metà parallelamente al bordo, si ottiene un altro nastro però con una torsione intera, due bordi e due superfici diverse, quindi orientabile. La cosa interessante è che i due bordi separati dalle forbici rimangono un solo bordo, quindi la figura viene completamente tagliata a metà, ma rimane attaccata;

Ora costruiamo un altro nastro di Möbius e proviamo a disegnare 2 linee parallele alla mediana, ma che dividono in 3 parti il nastro stesso; se tagliamo lungo tali linee  otteniamo 2 nastri di Möbius incatenati

Il nastro di Möbius ha però una cosa in comune con la superficie cilindrica considerata prima: entrambi hanno un bordo; osservando direttamente le superfici costruite, non è difficile convincersi che il bordo della superficie cilindrica è costituito da 2 circonferenze parallele tra loro, non giacenti sullo stesso piano, ma su piani paralleli. (Il bordo di una superficie di dimensione 2 e' sempre un oggetto di dimensione minore di 2, ovvero 1 o 0). Per il Nastro di Möbius invece, il bordo, se uno prova a seguirlo, è costituito da una sola linea chiusa, quello che in Matematica si chiama curva di Jordan

  

L’equazione le cui soluzioni rappresentano il nastro è la seguente:

x²y+yz²+y³-y-2xz-2x²z-2y²z=0